Simulate using your own Types

Author

Darren Irwin

Let’s build a simulation that uses our ability to define new data types (using the struct keyword). This will allow us to build parts of the simulation in an intuitive way, keeping us and our code organized.

Meiotic drive in a population

This example is from an analysis I did about meiotic drive, meaning when chromosomes (or parts of them) have a transmission advantage during meiosis. This violates the usual rules of Mendelian inheritance, in which alleles have a 50% probability of getting into offspring. There are many known examples of meiotic drive.

In female meiosis (i.e., egg production) in virtually all eukaryotes, the first cell division is asymmetric, with a large part of the cell becoming the egg and a small part becoming the polar body. If a chromosome gets into the egg it has the potential to be passed down into the next generation. If it is in the polar body, it does not get passed down. Spindle fibers leading to the egg differ molecularly than those leading to the polar body. This places selection on chromosomal variants that can somehow interact with the spindle fibers in such a way that they are more likely to get into the egg.

If some chromosomes have an advantage getting into eggs, then they will tend to spread through a population. But what if there is a cost to these meiotic drivers? Perhaps they cause some problem in terms of whole-organism fitness. If so, perhaps there are suppression mechanisms that would spread as well.

This situation is particularly intriguing in species with Z / W sex chromosomes (e.g., birds, butterflies), meaning females are ZW and males are ZZ. There, a driver on the W or Z can cause the sex ratio of a female’s offspring to be biased towards females (in the case of a W driver) or males (in the case of a Z driver). The figure below illustrates meiosis and the consequences of a W driver:

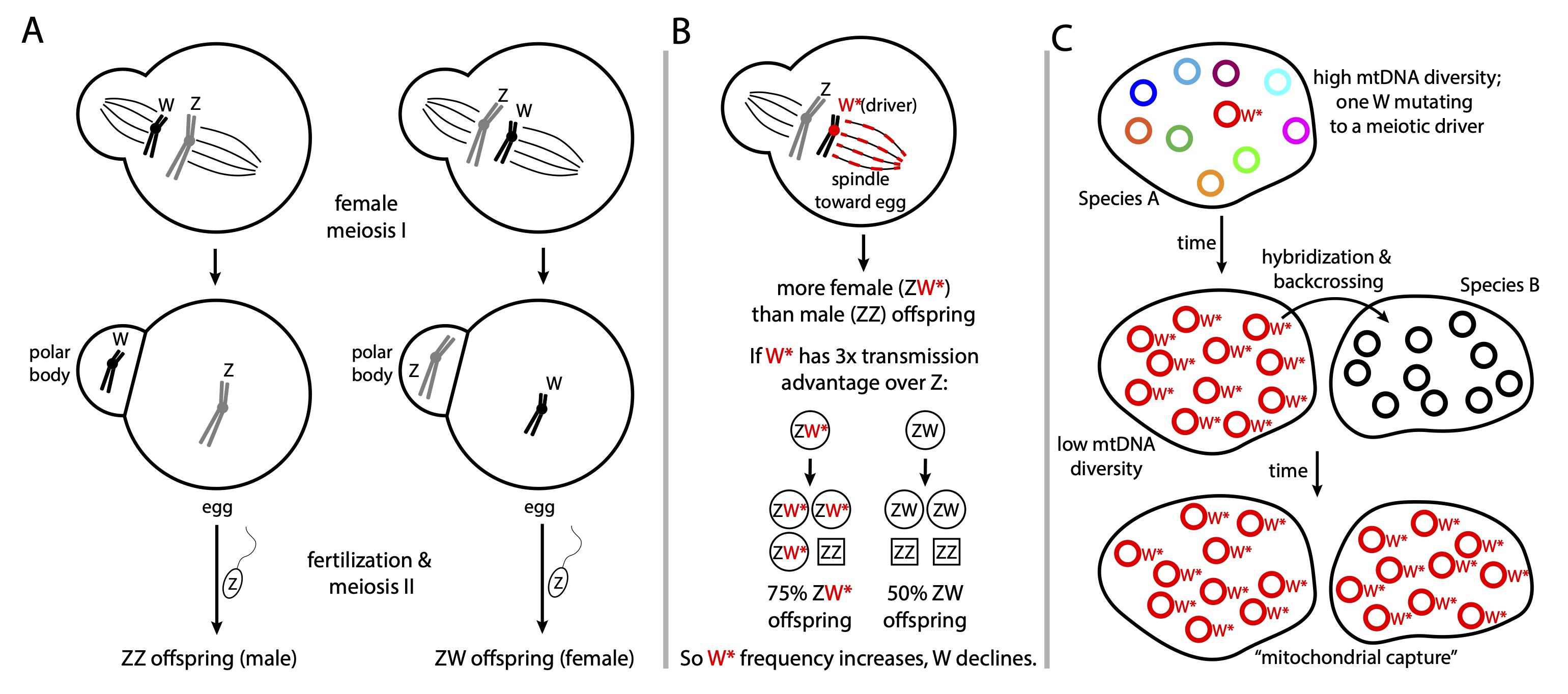
Transmission of the W chromosome via female meiosis, and the potential of a driving W to gain a bias in transmission, resulting in spread of the driving W and associated mitochondrial DNA (mtDNA). This is Figure 1 from Irwin 2025 BioRxiv.

The evolutionary dynamics of such a situation can be difficult to think through intuitively. So let’s build a simulation!

First step: consider data structures and the high-level logic of our program

Let’s consider how we can organize our simulation. One way is to invent new data types (structs) that store information at different levels, and then build functions that encapsulate the rules by which those data types interact.

So we’ll define new types for:

  • chromosomes (containing the kind of chromosome, its spindle attraction to the egg, its whole-organism fitness, and its ability to suppress drive)
  • individuals (containing 4 chromosomes: a sex chromosome and autosome inherited through the egg, and the same from the sperm)
  • populations (containing a bunch of female [ZW] individuals and a bunch of male [ZZ] individuals)

By setting up the above framework, we’ll be able to create functions that work with data at various levels, keeping everything well organized. Key functions will govern:

  • mating of two individuals, determining the chromosomes inherited by their offspring (i.e., new individuals)
  • breeding of one generation of a population, by choosing random parents for each offspring
  • survival of offspring to adulthood, based on fitness
  • recording frequencies of chromosome types and sexes in each generation
  • running many generations
  • graphing results

Defining our new types

Chromosomes

To store information for each chromosome, we’ll invent a Chrom type. It is convention in Julia for types to start with a capital letter (whereas functions start with lower case letters).

struct Chrom
    kind
    spindleAttraction # this means the strength of attraction to the egg (with 1.0 meaning a normal non-driver)
    # fitnessLoss (commented out, but we may want to add later)
    # suppressStrength (commented out, but we may want to add later)
end

Let’s now create some sex chromosomes, some with a drive advantage and some without:

driveStrength = 1.5  # sets this to be the drive strength of each driving chrom type
boringW = Chrom("W", 1.0) # a simple nothing-special W chromosome
drivingW = Chrom("W", driveStrength) # a driving W
boringZ = Chrom("Z", 1.0) 
# drivingZ = Chrom("Z", driveStrength)
Chrom("Z", 1.0)

Let’s add a simple autosome with nothing special:

boringAutosome1 = Chrom("1", 1.0)
Chrom("1", 1.0)
Individuals

We’ll define an Indiv type that has four chromosomes, and here we choose to specify that they must be of the Chrom type.

struct Indiv
    sexChromFromEgg::Chrom 
    sexChromFromSperm::Chrom
    autosome1FromEgg::Chrom
    autosome1FromSperm::Chrom
end

Now we can create some kinds of individuals, by specifying the four chromosomes according to the order above:

femaleBoring = Indiv(boringW, boringZ, boringAutosome1, boringAutosome1)
femaleDriveW = Indiv(drivingW, boringZ, boringAutosome1, boringAutosome1)
maleBoring = Indiv(boringZ, boringZ, boringAutosome1, boringAutosome1)
Indiv(Chrom("Z", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0))
Populations

Now we can create a data type that stores a whole population of females and males:

mutable struct Population
    popFemales
    popMales
end

We make this a mutable struct because the population will change over time (whereas each kind of chromosome and individual does not need to change after creation).

Create a starting population of 20000 individuals in which 5% of the W are driving:

pop1Females = vcat(fill(femaleDriveW, 500), fill(femaleBoring, 9500))
pop1Males = vcat(fill(maleBoring, 10000))
pop1 = Population(pop1Females, pop1Males)
Population(Indiv[Indiv(Chrom("W", 1.5), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("W", 1.5), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("W", 1.5), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("W", 1.5), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("W", 1.5), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("W", 1.5), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("W", 1.5), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("W", 1.5), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("W", 1.5), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("W", 1.5), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0))  …  Indiv(Chrom("W", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("W", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("W", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("W", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("W", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("W", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("W", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("W", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("W", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("W", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0))], Indiv[Indiv(Chrom("Z", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("Z", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("Z", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("Z", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("Z", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("Z", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("Z", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("Z", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("Z", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("Z", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0))  …  Indiv(Chrom("Z", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("Z", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("Z", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("Z", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("Z", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("Z", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("Z", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("Z", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("Z", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("Z", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0))])

We now have the main data structures needed for our simulations, so let’s define functions that do things with them.

Write a mating function

Our function will use the function sample() from the StatsBase package to make a random choice of chromosome to inherit, weighted by transmission probability. To download and install that package, if using the REPL, enter the package manager by typing ] and then type add StatsBase. Then, call that package into memory:

using StatsBase  # needed for "sample" function
TipPluto automatically installs packages

If using Pluto, you don’t need to explicitly add a package. Rather, using StatsBase will cause Pluto to download and install on first use. 😃

Given one female (ZW) and one male (ZZ) parent, we will write a function to determine the chromosomes passed on to one offspring, incorporating transmission advantage as calculated by the ratio of spindleAttraction of each chromosome compared to total spindleAttraction:

function makeOneOffspring(female, male) 
    # determine sex chromosome of egg, weighted by spindleAttraction
    transProbSexChromFromEgg = female.sexChromFromEgg.spindleAttraction / 
                    (female.sexChromFromEgg.spindleAttraction + female.sexChromFromSperm.spindleAttraction)
    eggSexChrom = sample([female.sexChromFromEgg, female.sexChromFromSperm], 
        Weights([transProbSexChromFromEgg, 1 - transProbSexChromFromEgg]))
    # determine sex chromosome of sperm, with no drive (Mendelian)
    spermSexChrom = sample([male.sexChromFromEgg, male.sexChromFromSperm])
    # determine autosome1 in egg, weighted by spindleAttraction
    transProbAutosome1FromEgg = female.autosome1FromEgg.spindleAttraction / 
                    (female.autosome1FromEgg.spindleAttraction +
                    female.autosome1FromSperm.spindleAttraction)
    eggAutosome1 = sample([female.autosome1FromEgg, female.autosome1FromSperm], 
                    Weights([transProbAutosome1FromEgg, 1 - transProbAutosome1FromEgg]))
    # determine autosome1 in sperm, Mendelian
    spermAutosome1 = sample([male.autosome1FromEgg, male.autosome1FromSperm])
    
    return Indiv(eggSexChrom, spermSexChrom, eggAutosome1, spermAutosome1)
end
makeOneOffspring (generic function with 1 method)

Let’s check that our function works:

makeOneOffspring(femaleDriveW, maleBoring)
Indiv(Chrom("Z", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0))

It does, but does it produce the transmission bias? Let’s build a test function to check that:

function test_makeOneOffspring(female, male, reps)
    offspringSex = fill("N", reps)
    for i in 1:reps
        kid = makeOneOffspring(female, male)
        if kid.sexChromFromEgg.kind == "W"
            offspringSex[i] = "F"
        else offspringSex[i] = "M"
        end
    end
    proportionFemale = (sum(offspringSex .== "F") / reps)
    println("Out of " * string(reps) * " offspring, the proportion female is " * string(proportionFemale))
end
test_makeOneOffspring (generic function with 1 method)

Now run some tests:

test_makeOneOffspring(femaleDriveW, maleBoring, 1_000_000)
Out of 1000000 offspring, the proportion female is 0.600461

For a W driver with driveStrength of 1.5, the above should result in about 50% more females than males, so a proportion of 0.6 female (and 0.4 male).

When a female has no driving chromosomes, then the proportion of females should be about 0.5:

test_makeOneOffspring(femaleBoring, maleBoring, 1_000_000)
Out of 1000000 offspring, the proportion female is 0.499748

Write a function to breed one generation

Since we have a function for producing one offspring (see above), we can call that repeatedly to make an entire new generation of offspring, with each offspring having a randomly chosen mother and father. In addition to random mating, here we will assume constant population size and non-overlapping generations.

function breedOneGeneration(population::Population; k = length(population.popFemales) + length(population.popMales))
    # can set the number of offspring (k) in function call, or leave out and it will set k according to the current population size
    offspringFemales = []
    offspringMales = []
    # cycle through offspring, choosing random parents
    for i in 1:k
        mother = sample(population.popFemales)
        father = sample(population.popMales)
        offspring = makeOneOffspring(mother, father)
        if offspring.sexChromFromEgg.kind == "W" # so offspring is female
            push!(offspringFemales, offspring)
        elseif offspring.sexChromFromEgg.kind == "Z" # so offspring is male
            push!(offspringMales, offspring)
        end
    end
    return Population(offspringFemales, offspringMales)
end
breedOneGeneration (generic function with 1 method)

Let’s test the above function with one generation of breeding of the pop1 that we created further above:

popNext = breedOneGeneration(pop1)
println("The offspring generation has ", string(length(popNext.popFemales)), " females and ", string(length(popNext.popMales)), " males.")
The offspring generation has 10086 females and 9914 males.

Write some functions for recording population proportions

function getPropDrivingW(population::Population)
    driving = []
    for i in population.popFemales # all females have a single W, making next line OK
        if i.sexChromFromEgg.spindleAttraction > 1.0
            push!(driving, true)
        else push!(driving, false)
        end
    end
    return sum(driving) / length(driving)
end
getPropDrivingW (generic function with 1 method)

Test this function:

getPropDrivingW(pop1)
0.05

Let’s also record the proportion of females:

function getPropFemale(population::Population)
    length(population.popFemales) / 
            (length(population.popFemales) + length(population.popMales))
end
getPropFemale (generic function with 1 method)

Try it:

getPropFemale(pop1)
0.5

Put it all together

We now have all the pieces to build a big-picture function that runs the simulation for many generations:

function runManyGens(population::Population, gens::Int; k = length(population.popFemales) + length(population.popMales))
    # The above sets k (the number of offspring in each generation) as the starting population size
    # Create vectors to store proportions over the generations:
    propFemale = fill(-0.9999, gens+1)      # Fill with obviously wrong values,
    propDrivingW = fill(-0.9999, gens+1)    # which will be written over as simulation proceeds.
    # record proportions in starting population (generation 0; index 1)
    propFemale[1] = getPropFemale(population)
    propDrivingW[1] = getPropDrivingW(population)
    # Loop through generations
    for i in 1:gens
        # produce offspring
        population = breedOneGeneration(population; k)
        # record proportions in the offspring generation
        propFemale[i+1] = getPropFemale(population)
        propDrivingW[i+1] = getPropDrivingW(population)
    end
    return (propFemale = propFemale, 
            propDrivingW = propDrivingW, 
            population = population)
end
runManyGens (generic function with 1 method)

The above function returns a tuple containing the record of female proportions over time, driving W proportions over time, and the final population.

Run the simulation!!

OK, we’ve done a lot of setup. Now lets run and see what happens. This will rely on the Plots package—if not installed yet and if you are using the REPL, enter the package manager by typing ] at the REPL prompt, then type add Plots.

using Plots
runLength = 100  # generations
pop1run = runManyGens(pop1, runLength)
pop1plot = plot(0:runLength, pop1run.propFemale, color = :purple, label = "Females", xlabel = "Generations", ylabel = "Proportion", title = "Driving W, Drive Strength = " * string(driveStrength))
xlims!(0, runLength)  # sets x axis limits
ylims!(0, 1.05)  # sets y axis limits
plot!(0:runLength, pop1run.propDrivingW, color = :red, label = "Driving W")

Our graph shows something not too surprising: the driving W (red line) spreads through the population rather quickly, and this causes the sex ratio to change from 50% to about 60% female.

You could play with the simulation by changing the value of driveStrength or the starting population size and frequency of the driving W.

Or, let’s try asking an interesting question: How fast would a driving Z (rather than W) spread? Would it have the same potential as a W to spread, or would it go faster or slower? If both a driving W and driving Z start at the same low frequency, what happens?

Add a driving Z

Because we’ve built our simulation above using data structures (types) and functions that are well-organized and quite general (not specific to the particular scenario in the graph above), it is easy for us to add another kind of chromosome and see what happens:

drivingZ = Chrom("Z", driveStrength)
Chrom("Z", 1.5)

This creates a Driving Z chromosome that has the equivalent drive strength as our Driving W above (a 50% advantage in getting into the egg, compared to a “boring” Z or W).

We can now make some new kinds of starting individuals, with respect to the driving Z chromosome:

femaleDriveZ = Indiv(boringW, drivingZ, boringAutosome1, boringAutosome1)
femaleDriveWZ = Indiv(drivingW, drivingZ, boringAutosome1, boringAutosome1)
maleFirstDriveZ = Indiv(drivingZ, boringZ, boringAutosome1, boringAutosome1)
maleSecondDriveZ = Indiv(boringZ, drivingZ, boringAutosome1, boringAutosome1)
maleTwoDriveZ = Indiv(drivingZ, drivingZ, boringAutosome1, boringAutosome1)
Indiv(Chrom("Z", 1.5), Chrom("Z", 1.5), Chrom("1", 1.0), Chrom("1", 1.0))

Now let’s make a population that has 5% starting Driving Z. This will be more complex than in the Driving W case, because there are more kinds of starting individuals. The code below set’s things up initially according to Hardy-Weinberg equilibrium (i.e. according to frequencies that would result from random mating):

pop2setPropDrivingZ = 0.05
pop2SizeFemale = 10_000
pop2SizeMale = 10_000
pop2Females = vcat(fill(femaleDriveZ, Int(round(pop2setPropDrivingZ * pop2SizeFemale))), 
                fill(femaleBoring, Int(round((1-pop2setPropDrivingZ) * pop2SizeMale))))
pop2numMaleTwoDriveZ = Int(round(pop2setPropDrivingZ^2 * pop2SizeMale))
pop2numMaleFirstDriveZ = Int(round(pop2setPropDrivingZ * (1-pop2setPropDrivingZ) * pop2SizeMale))
pop2numMaleSecondDriveZ = Int(round((1-pop2setPropDrivingZ) * pop2setPropDrivingZ * pop2SizeMale))
pop2numMaleBoring = Int(round((1-pop2setPropDrivingZ)^2 * pop2SizeMale))
pop2Males = vcat(fill(maleTwoDriveZ, pop2numMaleTwoDriveZ),
                fill(maleFirstDriveZ, pop2numMaleFirstDriveZ),
                fill(maleSecondDriveZ, pop2numMaleSecondDriveZ),
                fill(maleBoring, pop2numMaleBoring))
pop2 = Population(pop2Females, pop2Males)
Population(Indiv[Indiv(Chrom("W", 1.0), Chrom("Z", 1.5), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("W", 1.0), Chrom("Z", 1.5), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("W", 1.0), Chrom("Z", 1.5), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("W", 1.0), Chrom("Z", 1.5), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("W", 1.0), Chrom("Z", 1.5), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("W", 1.0), Chrom("Z", 1.5), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("W", 1.0), Chrom("Z", 1.5), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("W", 1.0), Chrom("Z", 1.5), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("W", 1.0), Chrom("Z", 1.5), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("W", 1.0), Chrom("Z", 1.5), Chrom("1", 1.0), Chrom("1", 1.0))  …  Indiv(Chrom("W", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("W", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("W", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("W", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("W", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("W", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("W", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("W", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("W", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("W", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0))], Indiv[Indiv(Chrom("Z", 1.5), Chrom("Z", 1.5), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("Z", 1.5), Chrom("Z", 1.5), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("Z", 1.5), Chrom("Z", 1.5), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("Z", 1.5), Chrom("Z", 1.5), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("Z", 1.5), Chrom("Z", 1.5), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("Z", 1.5), Chrom("Z", 1.5), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("Z", 1.5), Chrom("Z", 1.5), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("Z", 1.5), Chrom("Z", 1.5), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("Z", 1.5), Chrom("Z", 1.5), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("Z", 1.5), Chrom("Z", 1.5), Chrom("1", 1.0), Chrom("1", 1.0))  …  Indiv(Chrom("Z", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("Z", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("Z", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("Z", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("Z", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("Z", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("Z", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("Z", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("Z", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("Z", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0))])

We need to add a function for calculating the population proportion of the driving Z, so we can track that over the generations:

function getPropDrivingZ(population::Population)
    driving = []
    # have to cycle through females and males to count up all the driving Z
    for i in population.popFemales
        if i.sexChromFromSperm.spindleAttraction > 1.0
            push!(driving, true)
        else push!(driving, false)
        end
    end
    for i in population.popMales
        if i.sexChromFromEgg.spindleAttraction > 1.0
            push!(driving, true)
        else push!(driving, false)
        end
        if i.sexChromFromSperm.spindleAttraction > 1.0
            push!(driving, true)
        else push!(driving, false)
        end     
    end
    return sum(driving) / length(driving)       
end
getPropDrivingZ (generic function with 1 method)

Let’s also modify the runManyGens() funciton so that it keeps track of the driving Z frequency:

function runManyGens(population::Population, gens::Int; k = length(population.popFemales) + length(population.popMales))
    # The above sets k (the number of offspring in each generation) as the starting population size
    # Create vectors to store proportions over the generations:
    propFemale = fill(-0.9999, gens+1)      # Fill with obviously wrong values,
    propDrivingW = fill(-0.9999, gens+1)    # which will be written over as simulation proceeds.
    propDrivingZ = fill(-0.9999, gens+1)
    # record proportions in starting population (generation 0; index 1)
    propFemale[1] = getPropFemale(population)
    propDrivingW[1] = getPropDrivingW(population)
    propDrivingZ[1] = getPropDrivingZ(population)
    # Loop through generations
    for i in 1:gens
        # produce offspring
        population = breedOneGeneration(population; k)
        # record proportions in the offspring generation
        propFemale[i+1] = getPropFemale(population)
        propDrivingW[i+1] = getPropDrivingW(population)
        propDrivingZ[i+1] = getPropDrivingZ(population)
    end
    return (propFemale = propFemale, 
            propDrivingW = propDrivingW,
            propDrivingZ = propDrivingZ, 
            population = population)
end
runManyGens (generic function with 1 method)

Let’s now run the simulation with this starting population, and graph the results:

pop2run = runManyGens(pop2, runLength)
pop2plot = plot(0:runLength, pop2run.propFemale, color = :purple, label = "Female", xlabel = "Generations", ylabel = "Proportion", title = "Driving Z, Drive Strength = " * string(driveStrength))
xlims!(0,runLength)
ylims!(0, 1.05)
plot!(0:runLength, pop2run.propDrivingZ, color = :blue, label = "Driving Z")

This shows us something interesting: Equivalent strength W and Z drivers tend to spread through a population at different rates. The W spreads much more quickly. This is something that maybe some people would intuit in advance, and might be a surprise to many. Our simulation shows us this, and we can then ponder “Why?”

After some thought, we might realize the answer: All of the W chromosomes are in females, whereas only 1/3 of Z chromosomes are in females (assuming equal sex ratios). Because the meiotic drive advantage only applies in female meiosis (rather than male), the strength of selection for the W driver is much greater than that for the Z driver.

What happens when both Z and W drivers are in a population?

Let’s now start a population with both Z and W drivers at 5% initially. Might they both cancel out each other’s effects? (After all, when in the same pre-meiotic cell, neither has an advantage getting into the egg.)

Let’s see by running a simulation!

Our setup of the starting population is even a little more complex, because there are more kinds of starting individuals:

pop4setPropDrivingW = 0.05
pop4setPropDrivingZ = 0.05
pop4SizeFemale = 10_000
pop4SizeMale = 10_000

pop4numFemaleDriveWZ = Int(round(pop4setPropDrivingW * pop4setPropDrivingZ * pop4SizeFemale))
pop4numFemaleDriveW = Int(round(pop4setPropDrivingW * (1-pop4setPropDrivingZ) * pop4SizeFemale))
pop4numFemaleDriveZ = Int(round((1-pop4setPropDrivingW) * pop4setPropDrivingZ * pop4SizeFemale))
pop4numFemaleBoring = Int(round((1-pop4setPropDrivingW) * (1-pop4setPropDrivingZ) * pop4SizeFemale))

pop4Females = vcat(fill(femaleDriveWZ, pop4numFemaleDriveWZ),
                fill(femaleDriveW, pop4numFemaleDriveW),
                fill(femaleDriveZ, pop4numFemaleDriveZ),
                fill(femaleBoring, pop4numFemaleBoring))

pop4numMaleTwoDriveZ = Int(round(pop4setPropDrivingZ^2 * pop4SizeMale))
pop4numMaleFirstDriveZ = Int(round(pop4setPropDrivingZ * (1-pop4setPropDrivingZ) * pop4SizeMale))
pop4numMaleSecondDriveZ = Int(round((1-pop4setPropDrivingZ) * pop4setPropDrivingZ * pop4SizeMale))
pop4numMaleBoring = Int(round((1-pop4setPropDrivingZ)^2 * pop4SizeMale))
pop4Males = vcat(fill(maleTwoDriveZ, pop4numMaleTwoDriveZ),
                fill(maleFirstDriveZ, pop4numMaleFirstDriveZ),
                fill(maleSecondDriveZ, pop4numMaleSecondDriveZ),
                fill(maleBoring, pop4numMaleBoring))
pop4 = Population(pop4Females, pop4Males)
Population(Indiv[Indiv(Chrom("W", 1.5), Chrom("Z", 1.5), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("W", 1.5), Chrom("Z", 1.5), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("W", 1.5), Chrom("Z", 1.5), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("W", 1.5), Chrom("Z", 1.5), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("W", 1.5), Chrom("Z", 1.5), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("W", 1.5), Chrom("Z", 1.5), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("W", 1.5), Chrom("Z", 1.5), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("W", 1.5), Chrom("Z", 1.5), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("W", 1.5), Chrom("Z", 1.5), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("W", 1.5), Chrom("Z", 1.5), Chrom("1", 1.0), Chrom("1", 1.0))  …  Indiv(Chrom("W", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("W", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("W", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("W", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("W", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("W", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("W", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("W", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("W", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("W", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0))], Indiv[Indiv(Chrom("Z", 1.5), Chrom("Z", 1.5), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("Z", 1.5), Chrom("Z", 1.5), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("Z", 1.5), Chrom("Z", 1.5), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("Z", 1.5), Chrom("Z", 1.5), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("Z", 1.5), Chrom("Z", 1.5), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("Z", 1.5), Chrom("Z", 1.5), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("Z", 1.5), Chrom("Z", 1.5), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("Z", 1.5), Chrom("Z", 1.5), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("Z", 1.5), Chrom("Z", 1.5), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("Z", 1.5), Chrom("Z", 1.5), Chrom("1", 1.0), Chrom("1", 1.0))  …  Indiv(Chrom("Z", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("Z", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("Z", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("Z", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("Z", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("Z", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("Z", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("Z", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("Z", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0)), Indiv(Chrom("Z", 1.0), Chrom("Z", 1.0), Chrom("1", 1.0), Chrom("1", 1.0))])

Now, let’s run it:

pop4run = runManyGens(pop4, runLength)
pop4plot = plot(0:runLength, pop4run.propFemale, color = :purple, label = "Female", xlabel = "Generations", ylabel = "Proportion", title = "Driving W and Z, Drive Strength = " * string(driveStrength))
xlims!(0, 100)
ylims!(0, 1.05)
plot!(0:runLength, pop4run.propDrivingW, color = :red, label = "Driving W")
plot!(0:runLength, pop4run.propDrivingZ, color = :blue, label = "Driving Z")

Here, we see that the driving Z has little ability to hinder the spread of the driving W. Rather, the driving W still spreads quickly, going to fixation, and the driving Z spreads more slowly. We see that the sex ratio becomes female-biased as the driving W spreads, but eventually returns to 50:50 when the driving Z goes towards fixation.

The net effect is that W drivers have great potential to spread, and these can be followed by Z drivers, returning the sex ratio to an unremarkable level. The insight then from these simulations is that spread of W and Z drivers can occur regularly within species, and we might not notice.